论文链接 NEVER GIVE UP:LEARNING DIRECTED EXPLORATION STRATEGIES

概要

提出一种intrinsic reward来引导智能体进行探索，在Atari-57中探索困难的游戏上都取得了两倍以上的分数，同时在其他游戏上也保持了很高的分数。这个新提出的算法在Pitfall!这个游戏上首次不依赖人类经验或手工设计的特征而取得非0分数。

问题

探索问题一直是深度强化学习中的一个巨大挑战，通常一个算法需要对所有状态-动作的pair都探索到一定次数，才能保证找到最优策略。但往往策略会在学习一定步数之后表现出对局部奖励的偏好，导致其行动受到影响，无法收集到足够丰富的经验来学习。最简单的办法是使用$\epsilon$-greedy或Boltzmann探索，这些方法虽然低效，但在部分reward稠密的环境下也取得了很好的效果。不过，在稀疏reward的环境下，这些策略就行不通了。

现状

目前有多种基于intrinsic reward来鼓励agent探索的研究。这种reward与一个状态的新奇程度成正比，当探索的状态足够多时各个状态不再新奇，也就不提供reward了，从而policy就会开始专注于优化外界奖励。这种方式在一些难探索的环境上取得了很好的效果，但它本质上的缺陷在于对于一个状态只关心它本身的新奇程度而忽略了它下游状态的新奇程度。还有一种方式则是通过对状态可预测性来间接表现状态的新奇程度，预测误差越大奖励越大。但学习一个状态的预测模型本身很有一定的成本，模型的误差会有较大影响，而且也很难在任意环境上使用。

新方法

作者基于UVFA(Universal Value Function Approximators)提出了用同一个网络同时学习多个具有不同探索倾向的policy的想法。并且提出了一个intrinsic reward来结合回合内的探索奖励与agent整个生命周期内的探索情况。

算法

THE NEVER-GIVE-UP INTRINSIC REWARD

在NGU中,reward的由外在reward和内在reward的线性组合构成。 $r_t=r_t^e+\beta r_t^i$，$r_t^e$表示外在奖励,$r_t^i$表示内在奖励，$\beta$ 是一个正常数，用于调整两种reward的影响。

$r_t^i$的计算公式为:

\[r_t^i=r_t^{episodic}·min\{max\{\alpha_t,1\},L\}\]

$r_t^{epsilon}$表示回合内的探索奖励，$\alpha_t$为生命周期内的好奇心因子。 其中$min\{max\{\alpha_t,1\},L\}$这部分用于限制$\alpha_t$的范围在1到L之间，作者在本文的所有实验中设置了L=5。

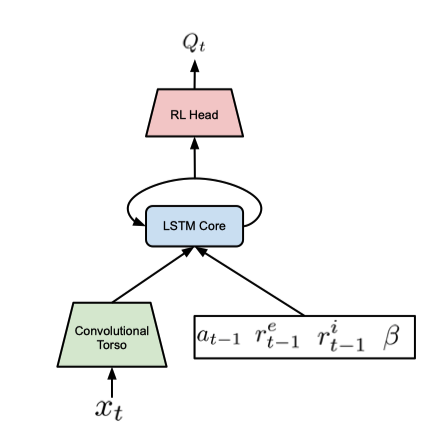
它的计算流程如下图所示。

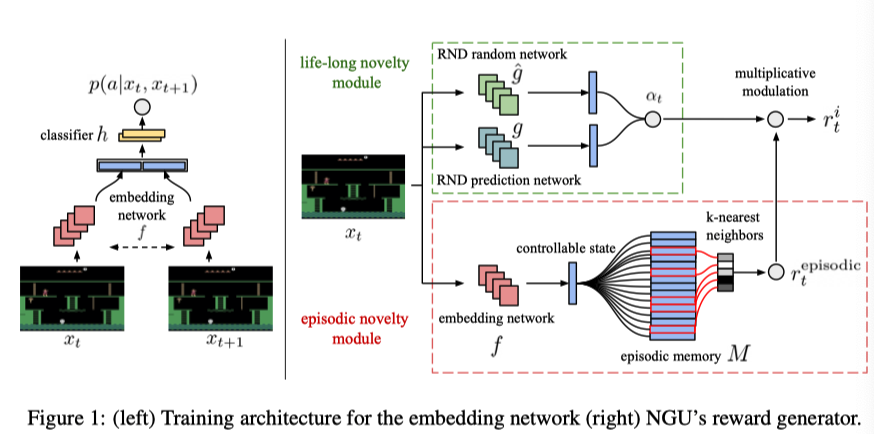
下面依次介绍图中各个组件。

1. Embedding network

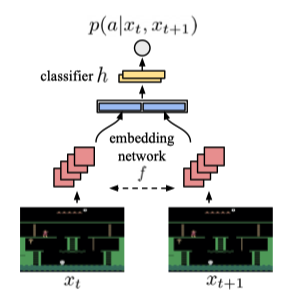
Embedding network $f$用于将observation映射成低维的向量，这个向量对应于可控制的状态。强调’可控’的原因是，对于状态自身会随时间改变的环境(作者举了一个交通状况的例子，即使什么都不做，也可以观测到大量不同的observation)，这种形式的状态探索和动作的探索性没有关系，也就不应该为该动作提供探索奖励。为此，作者通过训练一个孪生网络来预测状态改变与动作的关系，以剔除与动作对环境的影响无关的因素。如图所示，两个孪生网络接受先后两个observation，它们的输出会拼接在一起，输入一个含一层隐藏层的全连接神经网络分类器$h$正式的表示:为对于一条经验$\{x_t,a_t,x_{t+1}\}$，分类器输出概率 $ p(a|x_t,x_{t+1})=h(f(x_t),f(x_{t+1}))$, 然后通过最大似然优化$f$与$h$两个网络的参数。

2. Episodic memory and intrinsic reward

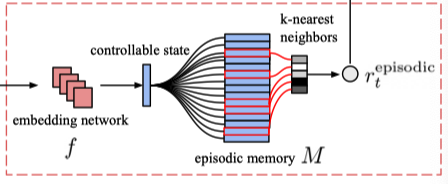
在每一个回合中，提供一个大小可变的记忆单元$M$,用于存储可控状态(即$f(x_t)$)。 定义回合内探索奖励为:

\[r_t^{episodic}=\frac{1}{\sqrt{n(f(x_t))}}\approx \frac{1}{\sqrt{\Sigma_{f_i \in N_k}K(f(x_i),f_i))}+c}\]

其中，$n(f(x_t))$表示之前访问抽象状态$f(x_t)$的次数，然后作者使用由核函数$K:\mathbb{R}^p\times \mathbb R^p \rightarrow \mathbb{R}$计算出的相似值的和来近似这个次数。c是一个常数，用来作为最小的访问次数(在本文所有实验中固定使用$10^{-3}$)。$N_k$为$M$中的$k$个与$f(x_t)$距离最近的抽象状态。

\[K(x,y)=\frac{\epsilon}{\frac{d^2(x,y)}{d^2_m}+\epsilon}\]

$\epsilon$是一个极小的常数，在本文所有实验中固定为$10^{-3}$，$d$是欧式距离，$d_m^2$是欧式距离平方值的滑动平均。

3. Integrating life-long curiosity

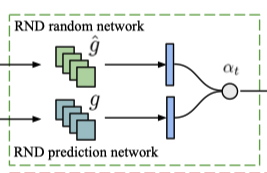
原则上，一切评估了长期新奇度的度量都可以作为$\alpha_t$的基准。作者借鉴Random Network Distillation(RND)的研究，使用了一个随机初始化的网络$g:\mathcal{O}\rightarrow \mathbb R^k$，然后训练另一个网络$\hat g:\mathcal{O}\rightarrow \mathbb R^k$ 来预测$g$的输出，最小化预测误差 $err(x_t)=||\hat g(x_t;\theta)-g(x_t)||^2$。 $\alpha_t$定义为正则化后的预测误差:

\[\alpha_t=1+\frac{err(x_t)-\mu_e}{\theta_e}\]

其中$\theta_e$和$\mu_e$分别为$err(x_t)$的滑动标准差和滑动均值。

THE NEVER-GIVE-UP AGENT

基于上一部分讲到的reward设计，现在的reward不再是只受action和state影响的随机变量了，因此目前agent实际上面临的是一个POMDP(partially Observed MDP)问题。为了简单处理，agent维护一个内部状态用来记忆历史信息(即使用RNN)。本文中作者使用了R2D2。

另外，由于探索奖励直接融合到了agent的奖励中，所以policy的探索偏好已经被刻入其学到的价值函数中，无法轻易的关闭。为了解决这个问题，作者会同时训练一个只接受外在环境奖励的policy。

训练架构

通过Universal value function approximator(UVFA)的方式，学习一个函数$Q(x,a,\beta_i)$来近似在不同的回报 $r_t^{\beta_i}=r_t^e+\beta_i r_t^i$ 下的最优价值函数。 $\beta$属于离散集合 $\{\beta_i\}_{i=0}^{N-1}$

该集合中包含了$\beta_0=0$ 和$\beta_{N-1}=\beta$ ，$\beta = max\{\beta_i\}_{i=0}^{N-1}$

通过这种方式,便可以通过将$\beta$设置为0来关闭policy的探索行为。

Loss

使用了transformed Retrace double Q-learning loss。

\[L(x_t,a_t,\theta)=(Q(x_t,a_t;\theta)-\hat y_t)^2\] \[\hat y_t = h(h^{-1}(Q(x_t,a_t;\theta^-)) +\sum_{s=t}^{t+k-1} \gamma^{s-t}(\prod_{i=t+1}^s c_i)(r_s+\gamma \sum_{a \in A} \pi(a|x_{s+1})h^{-1}(Q(x_{s+1},a;\theta^-))-h^{-1}(Q(x_s,a_s;\theta^-))))\] \[c_s=\lambda min(1,\frac{\pi(a_s|x_s)}{\mu(a_s|x_s)})\] \[h(z) = sign(z)(\sqrt{\|z\|+1}-1)+\epsilon z, \space \epsilon=10^{-2}\] \[h^{-1}(z) = sign(z)((\frac{\sqrt{1+4 \epsilon(|z|+1+\epsilon)}-1}{2 \epsilon})^2-1)\]

(本论文附录E中的$h^{-1}(z)$有误，以Observe and Look FurtherA.2中的公式为准。)

transformed Retrace double Q-learning loss其实是transformed bellman operator, Retrace和Double Q-learning的结合。 h函数和transformed bellman operator是在Observe and Look Further这篇论文中提出的。 Double Q-learning应该就不需要多说了，已经非常常见了。 Retrace是一种借鉴资格迹方法提出的根据多步经验平滑Q值估计的方法，可以减小Q值的方差。

另外，对于不同的$\beta_i$，作者设置了不同的折扣率$\gamma_i$。偏好探索的policy应该具有更小的折扣率，偏好利用的policy应该有更大的折扣率。本文的实验中，$\gamma_0=\gamma_{max}=0.997$,$\gamma_{N-1}=\gamma_{min}=0.99$。

分布式训练

采用Ape-X的方式，将learner与actor解耦。 learner仅有一个，负责优化价值函数，embedding function和RND predictor.

actor有多个，负责并行的收集经验数据。

实现细节

训练过程中，每个actor具有不同的$\beta$和$\gamma$值，并且采用$\epsilon$-greedy策略。

对于第i个actor，它的$\beta$设置为

\[\beta_i=\left\{ \begin{aligned} 0 & &i = 0 \\ \beta & & i = N-1 \\ \beta·\sigma(10\frac{2i-(N-2)}{N-2}) & & other \end{aligned} \right.\]

它的$\gamma$设置为

\[\gamma_i=1-exp(\frac{(N-1-i)\log(1-\gamma_{max})+i\log(1-\gamma_{min})}{N-1})\]

replay buffer中的设置与R2D2相同，每条经验为长度为80的(x,a,r)元组，前后两条经验有40个time-steps的重叠。一条经验不会跨越两个episode。

其他还有大量的网络结构，超参数设置都在论文的附录中，这里就不一一摘抄了。

分析

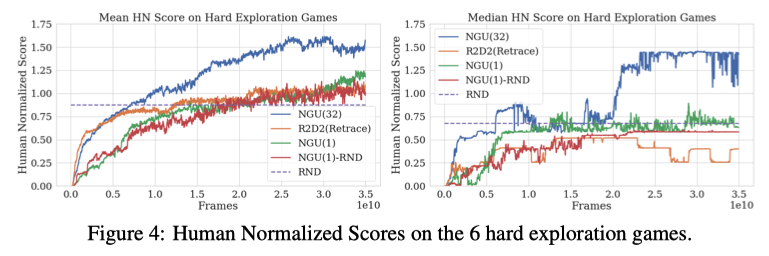
作者在6个难以探索的游戏环境上进行了实验对比，结果表明NGU大幅的提高了agent的表现。

总结

The proposed agent achieves high scores in all Atari hard-exploration games, while still maintaining a very high average score over the whole Atari-57 suite.

NGU大幅的的提高了agent在难以探索的游戏环境中的表现，同时在其他环境让也保持了非常高的水准。

但是NGU算法提高了采样的复杂度，相比之前的算法需要更多的样本。

此外，本算法提出的可控状态的计算方式不一定适用于所有环境，比如对于某些环境，action对环境变化的影响并不会即时生效，要在多个步数之后才得以体现。

最后，超参数$\beta$是用来平衡探索奖励和环境奖励的，因此它的值取决于外界奖励的大小，需要针对环境进行调整。