论文链接 Human-level Atari 200x faster

概要

DeepMind(DM)之前提出的Agent57算法成为了第一个能在所有(57个)Atari游戏上全面超过人类水平，但其样本利用率很低。新提出的MEME(MEME is an Efficient Memory-based Exploration agent)算法从四个角度进行了改进，在不影响性能的前提下，使用的环境样本减少到了原来的1/200。

问题

在Agent57的基础上,DM希望提升算法对样本的利用效率，在保证算法性能的前提下尽可能的减少与环境交互的次数。

方法

A.增强稀有事件下学习信号的传递和利用

A1 提升online网络的引导信号

target网络是一种常用的技术，用来限制目标值的变化速度，从而稳定价值函数的拟合目标，帮助网络对动态目标进行拟合。但这一技术的负面影响在于限制了网络的学习速度，因为拟合的目标是由target网络产生的，而他总是落后于最新的(通常也是更准确的)current(也可以叫做online)网络的值。通常，我们会通过调整target网络的更新频率和更新幅度来权衡这一对利弊关系。在本文中，为了能提升学习信号的传递速率，作者提出了一种近似置信域(approximate trust region)方法来稳定学习过程，从而让target网络可以进行更快，更大幅度的更新，而不影响训练的稳定性。

置信域方法的思想是对样本进行筛选，去除对于更新方向有较大干扰的样本。其筛选条件如下:

\[|Q^j(x_t,a_t;\theta) - Q^j(x_t,a_t;\theta_T)| > \alpha\sigma_j \space (1)\] \[sgn(Q^j(x_t,a_t;\theta) - Q^j(x_t,a_t;\theta_T)) \neq sgn(Q^j(x_t,a_t;\theta) - G_t) \space(2)\]

其中 $alpha$ 是一个固定的超参数，$G_t$ 是对return的估计， $ \theta$, $\theta_T$ 是current网络和target网络的参数, $\sigma_j$ 是TD-error的标准差。

式(1)会筛选出current网络与target网络的输出相差过大的样本，式(2)会筛选出current网络朝target网络更新的方向与朝着真实轨迹下计算的return方向不统一的样本，如果一个样本同时满足这两个条件，则认为它在置信域之外，从而不使用它进行更新。

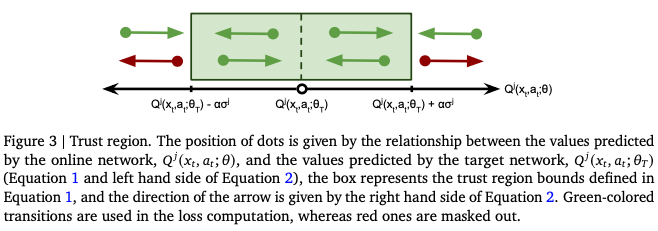
如图所示，红色的点的更新方向与真实return的方向相反两个网络的差值过大，所以被mask掉，不参与更新。

通过这个方法，虽然target网络变化更快了，但由于提出了对梯度方向影响较大的一些特殊样本，因而整体上缓和了拟合目标的变化速度，既利用了更新的网络参数，又稳定了学习过程，

A2 对贪心动作容忍度更高的Target值计算策略

Agent57中使用了Retrace技术来对return进行估计，但由于retrace方法会截断大于1的重要性采样的值,作者认为这个方法对使用 $\epsilon-greedy$ 的策略的裁剪过于激进了，阻碍了长期奖励信号的传递，于是提出了Soft Watkins $Q(\lambda)$方法。

这个方法对return的估计为:

\[G_t = max_a Q(x_t,a)+\sum_{k\ge 0}(\prod_{i=0}^{k-1}\lambda_i)\gamma^k(r_{t+k}+\gamma max_a Q(x_{t+k+1},a)-max_a Q(x_{t+k},a))) \space (3)\] \[\lambda_i = \lambda\mathbb{E}_{a\sim\pi(a|x_i)}[\mathbb{1}_{[Q(x_t,a_t;\theta)\ge Q(x_t,a;\theta) - \kappa|Q(x_t,a;\theta)|]}] \space (4)\]

其中 $\mathbb{1}$为指示函数，下标为真时值为1，反之值为0.

乍一看这个算式有点复杂，但我们以Watkins $Q(\lambda)$ 做为基础开始理解会比较简单。

对于Watkins $Q(\lambda)$ 他会在第一次选择非贪心动作事把迹向量清零。

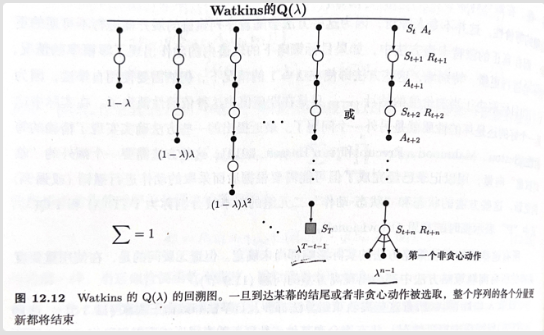
其实这个操作在等价与(3)式中在贪心时 $\lambda_i$ 取 $\lambda$ ，非贪心时 $\lambda_i$ 取0。 对于(4)式，我们可以先其在考虑的 $\kappa=0$ 且 $\pi$ 为贪心策略时意义。

(4)式中计算期望的部分

\[\mathbb{E}_{a\sim\pi(a|x_i)}[\mathbb{1}_{[Q(x_t,a_t;\theta)\ge Q(x_t,a;\theta) - \kappa|Q(x_t,a;\theta)|]}]\]

可以理解在判断来自采样轨迹中的动作 $a_i$ 是否是贪心动作,当他是贪心动作时，这个期望值为1，不是时则为0。可见， $\kappa=0$ 且 $\pi$ 的情况下，(4)式计算的 $\lambda_i$ 就是Watkins $Q(\lambda)$ 使用的 $\lambda_i$。

再看当 $\kappa \in (0,1)$时，那

\[\mathbb{E}_{a\sim\pi(a|x_i)}[\mathbb{1}_{[Q(x_t,a_t;\theta)\ge Q(x_t,a;\theta) - \kappa|Q(x_t,a;\theta)|]}]\]

这个期望值就不会严格要求 $a_i$ 是贪心动作了，对于非贪心但于最优动作差距不大(Q值差距不超过 $ \kappa|Q(x_t,a;\theta)| $ )的动作，其期望是非零的。这也就是soft这个词代表的含义。

这就相当于在Watkins $Q(\lambda)$ 的基础上，允许一部分采用了较好的非贪心动作的样本可以传导前后状态间的奖励信号，从而也就增加了样本的利用效率。

B. 稳定在不同奖励范围下的学习过程

B1 Loss 和 priority 的正则化

在MEME中，奖励的计算与Agent57一致，对每一个$policy_j$，其奖励$ r_{j,t}=r^e_t+\beta_j r^i_t$。

由于intrinsic/extrinsic reward( $r^i/r^e$) 的不同，每个$policy_j$的探索偏好$\beta_j$和折扣系数$\gamma_j$都不同,导致Q值会在一个相当大的范围内变化，这也就意味着绝对值大的Q值更容易主导训练，而对绝对值小的Q值的学习会更不稳定。特别对于extrinsic reward较小的环境，其影响更为严重。

对于这个问题作者提出了一个对TD-error的正则化的方法，用于平衡各个样本的loss和priority差别。这个方法通过对每个$policy_j$的TD-error计算running std $\sigma^{running}_j$和 batch std $\sigma^{batch}_j$。最后计算$\sigma_j=\max(\sigma^{running}_j, \sigma^{batch}_j,\epsilon)$。这个$\epsilon$的作用是设置一个下限，避免TD-error过小时会导致放大一些噪声信号，在MEME的实验中$\epsilon$统一取为0.01。最后，在计算loss和priority时，用TD-error除以$\sigma_j$的值即可。

B2 混合不同policy的经验进行交叉训练

在Agent57中，每一个$policy_j$收集的经验只会用来训练自身，因此很容易想到如果把所有policy一起训练应该能提升数据利用率。因此作者在原来的loss基础上融入了在其他policy上计算的loss，从而对所有policy一起训练。新的loss计算方式如下:

\[L=\eta L_{j_\mu}+\frac{1-\eta}{N}\sum^{N-1}_{j=0}L_j\]

其中$j_\mu$代表采样这条经验的策略,$L_j$表示$policy_j$的loss。$\eta$是用于混合各策略loss的超参数，作者发现取$\eta=0.5$的效果不错。

另外，为了提升计算效率，修改了原始的UVFA网络结构。在之前的结构中,网络会根据输入中的policy序号输出对应的Q值，现在由于需要同事计算各个policy的输出，于是修改为，不输入policy序号，而是在输出端同时输出所有policy的Q值，从而提高计算的并行性。

C. 神经网络结构改进

C1 Normalizer-free torso network

作者在实验中发现normalization layer对Agent57的网络性能有害，于是将其中使用的ResNet改为了新提出的NFNet网络，从而避免进行batch normalization操作。在NFNet中使用了自适应梯度裁剪（AGC)方法，不同于通常的梯度裁剪使用一个固定模长作为梯度向量的阈值，AGC中会根据权重的大小来动态调整这一阈值，实验证明这一方法确实有效。

另外采用了Deep networks with stochastic depth中提出的随机深度的方式进行训练，经增加了深层网络对梯度的传播能力，同时降低了网络的过拟合。这里需要注意的是，在计算多步回报时使用不同深度的网络会引入更高的方差，所以对同一条样本轨迹处理时会使用相同深度的网络，作者把这个网络深度的控制算法称为temporally-consistent stochastic depth mask。

C2 网络参数共享

在Agent57中，作者把NGU的Q网络拆成了$Q_e$,$Q_i$，来分别拟合extrinsic/intrinsic return。在本文中，作者指出这个方法会有更大的计算量，从而间接影响样本利用率。

另外作者指出了分开拟合和求和后拟合这两种情况的梯度是不同的，所以在函数近似时不能保证收敛到最优$Q^*$:

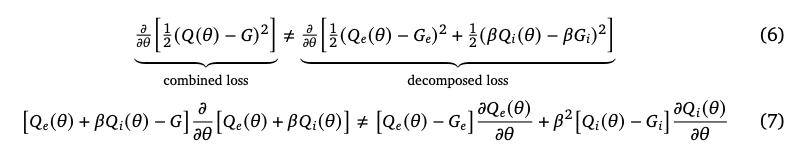
展开上图中的(7)式可以看到，左边多出的部分为:

\[\beta(Q_i(\theta)-G_i)\frac{\partial Q_e(\theta)}{\partial\theta} + \beta(Q_e(\theta)-G_e)\frac{\partial Q_i(\theta)}{\partial\theta}\]

这样看来，这些交叉项意味着在combined loss中$Q_e$和$Q_i$分别去填补了对方的loss，从而减小总体的loss。但我认为这多出的两项梯度会增加网络的拟合难度，至于究竟是共享网络提升的效率大，还是分开网络避免梯度交叉项提升的效率大，在Agent57中的说法和本文是相反的。

Agent57中作者如是说:

As a consequence, the conditional state-action value network of NGU is required to represent very different values depending on the $β_j$ we condition on. This implies that the network is increasingly required to have more flexible representations. Using separate networks dramatically increases its robustness to the intrinsic reward weight that is used.

本文中作者如是说:

While the form of the decomposition in Agent57 was chosen so as to ensure convergence to the optimal value-function $Q^*$ in the tabular setting, this does not generally hold under function approximation. Comparing the combined and decomposed losses we observe a mismatch in the gradients du to the absence of cross-terms in the decomposed loss

终归还是以实验结果为准，在后续的消融实验中证明了combine loss的效果更好，那就认为combine loss更适合吧。

D. 在policy快速变化的情况下进行稳定的更新

在2022年DM的一项研究The phenomenon of policy churn中，发现了 policy churn这一现象，指在DoubleDQN与R2D2等常见算法中，单次 Q network的更新会造成近10%的state上的greedy action发生改变。这一剧烈的策略变化会导致bootstrap的值会有较大的抖动，从而增大return的方差，减弱学习的稳定性。另外还会导致A1使用的trust region方法裁剪掉大量的样本，降低样本利用率。

针对这个问题，MEME中对每个policy增加了一个policy head,也就是说现在的网络不仅要输出N个policy的Q值，还要输出每个policy的动作分布，这个动作分布通过策略蒸馏的方式进行学习，并通过限制这个策略分布的每次优化后的变化量来增加策略的连续性，从而缓解前面提出的问题。

在策略蒸馏的其损失函数如下:

\[L_\pi = - \sum_{a,t}\mathcal{G}_\epsilon(Q(x_t,a;\theta))log\pi_{dist}(a|x_t;\theta)\space\forall t\space s.t.\space KL(\pi_{dist}(a|x_t;\theta_T)||\pi_{dist}(a|x_t;\theta))\le C_{KL}\]

可以看出policy head的拟合目标是$\epsilon$-greedy策略, 并且去除与target网络的动作的KL散度相差过大的一部分样本。

最终，在A1中的Soft Walkins $Q(\lambda)$中，target policy 使用的是$\pi_{dist}’=softmax(\frac{log \pi_{dist}}{\tau})$,其中$\tau$是一个温度变量，作者发现在[0,1]之前会有较好的效果，在接近1时训练更稳定，接近0时学习效率更高，最终取了$\tau=0.25$。

算法效果

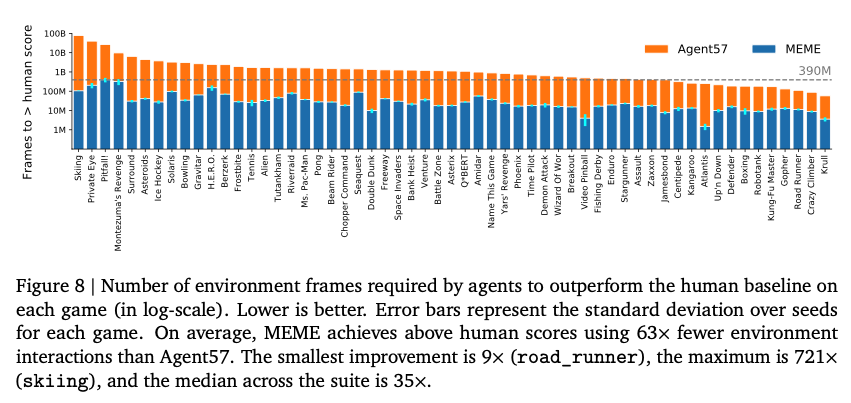
在57个Atari游戏上，MEME都取得了更好的数据利用率。

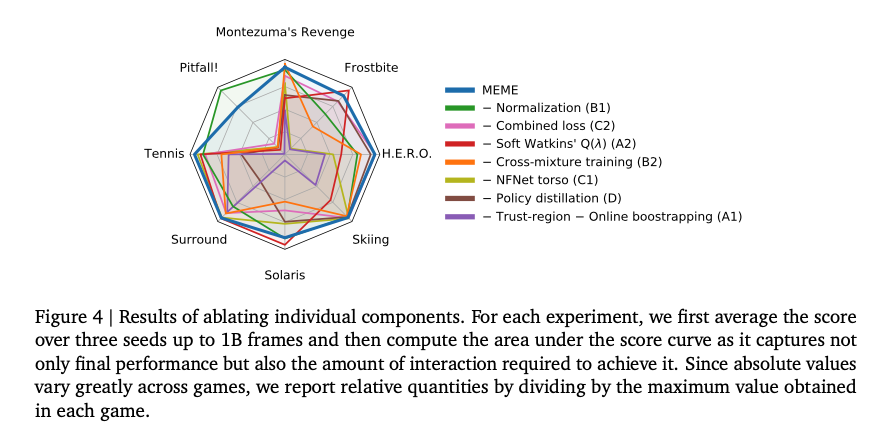
针对本文提出的几个改进，作者做了消融实验，可以看出每个改进点均对效果有所贡献，效果最明显的是A1的Trust region。

总结

本文提出的MEME方法在Agent57的基础上，对其在样本利用率进行了优化，从多个方面进行了或理论或实践的分析，并提出了有效的优化方法，不仅是这些改进点有参考价值，产生这些改进优化的分析思考方式同样是值得学习的。